library(caret) # The caret package
library(tidymodels) # Suite of packages for tidymodeling (eg. parsnip, recipes, yardstick, etc.)
library(tidyverse) # Suite of packages for tidy data science
library(skimr) # Package for summary stats on datasets
library(cowplot) # for making multi-paneled plots
options(width = 100) # ensure skim results fit on one lineI will be relying heavily on this website. My goal will be to record basic vignettes for common machine learning algorithms using caret…so that I don’t have to keep looking it up everytime I re-try something 😜. With tidymodels in active development, I also want to show how to implement the same caret code into tidymodels.
Initial Setup and Load Data Set
The goal of this dataset is to predict which of the two brands of orange juices did the customers purchase: Citrus Hill (CH) or Minute Maid (MM).
The predictor variables are characteristics of the customer and the product itself. It contains 1070 rows with 18 columns. The response variable is Purchase.
# Create data directory
if(!dir.exists("data/raw")){
dir.create("data/raw", recursive = TRUE)
}
# Download data set (if doesn't already exist)
if(!file.exists("data/raw/orange_juice_withmissing.csv")){
data_url <- "https://raw.githubusercontent.com/selva86/datasets/master/orange_juice_withmissing.csv"
dest_file <- "data/raw/orange_juice_withmissing.csv"
download.file(url = data_url, destfile = dest_file)
}
# Read in the data set
orange <- suppressMessages(suppressWarnings(read_csv("data/raw/orange_juice_withmissing.csv")))
# Summarize orange data
skim(orange)## Skim summary statistics
## n obs: 1070
## n variables: 18
##
## ── Variable type:character ───────────────────────────────────────────────────────────────────────────────────────────────────────
## variable missing complete n min max empty n_unique
## Purchase 0 1070 1070 2 2 0 2
## Store7 0 1070 1070 2 3 0 2
##
## ── Variable type:numeric ─────────────────────────────────────────────────────────────────────────────────────────────────────────
## variable missing complete n mean sd p0 p25 p50 p75 p100 hist
## DiscCH 2 1068 1070 0.052 0.12 0 0 0 0 0.5 ▇▁▁▁▁▁▁▁
## DiscMM 4 1066 1070 0.12 0.21 0 0 0 0.23 0.8 ▇▁▁▂▁▁▁▁
## ListPriceDiff 0 1070 1070 0.22 0.11 0 0.14 0.24 0.3 0.44 ▂▂▂▂▇▆▁▁
## LoyalCH 5 1065 1070 0.57 0.31 1.1e-05 0.32 0.6 0.85 1 ▅▂▃▃▆▃▃▇
## PctDiscCH 2 1068 1070 0.027 0.062 0 0 0 0 0.25 ▇▁▁▁▁▁▁▁
## PctDiscMM 5 1065 1070 0.059 0.1 0 0 0 0.11 0.4 ▇▁▁▂▁▁▁▁
## PriceCH 1 1069 1070 1.87 0.1 1.69 1.79 1.86 1.99 2.09 ▂▅▁▇▁▁▅▁
## PriceDiff 1 1069 1070 0.15 0.27 -0.67 0 0.23 0.32 0.64 ▁▁▂▂▃▇▃▂
## PriceMM 4 1066 1070 2.09 0.13 1.69 1.99 2.09 2.18 2.29 ▁▁▁▃▁▇▃▂
## SalePriceCH 1 1069 1070 1.82 0.14 1.39 1.75 1.86 1.89 2.09 ▁▁▁▂▆▇▅▁
## SalePriceMM 5 1065 1070 1.96 0.25 1.19 1.69 2.09 2.13 2.29 ▁▁▃▃▁▂▇▆
## SpecialCH 2 1068 1070 0.15 0.35 0 0 0 0 1 ▇▁▁▁▁▁▁▂
## SpecialMM 5 1065 1070 0.16 0.37 0 0 0 0 1 ▇▁▁▁▁▁▁▂
## STORE 2 1068 1070 1.63 1.43 0 0 2 3 4 ▇▃▁▅▁▅▁▃
## StoreID 1 1069 1070 3.96 2.31 1 2 3 7 7 ▃▅▅▃▁▁▁▇
## WeekofPurchase 0 1070 1070 254.38 15.56 227 240 257 268 278 ▆▅▅▃▅▇▆▇Convert to Factors
Some columns are shown as integers, but they need to be factors (eg. Purchase, Store7)
orange <- orange %>%
mutate(Purchase = as.factor(Purchase)) %>%
mutate(Store7 = as.factor(Store7)) %>%
mutate(StoreID = as.factor(StoreID))Splitting the Data (Train and Test)
caret::createDataPartition()
This will split the data on a based on a defined percentage that will be allocated to the training data:
set.seed(1234)
# Step 1: Get row numbers for the training data
trainRowNumbers <- createDataPartition(orange$Purchase, p = 0.75, list = FALSE)
# Step 2: Create the training dataset
trainData <- orange[trainRowNumbers,] # 75% of the data
# Step 3: Create the test dataset
testData <- orange[-trainRowNumbers,]
# Store X and Y for later use.
x <- trainData[, 2:18]
y <- trainData$Purchasersample::initial_split()
Same thing as above but using the rsample package from tidymodels:
set.seed(1234)
# Split data into training and test data
orange_split <- initial_split(orange, prop = 0.75)
train_data <- training(orange_split)
test_data <- testing(orange_split)Note that despite setting the same seed, the training data sets are different. I’ll work with the createDataPartition() train/test data sets moving forward.
rm(orange_split, train_data, test_data)
skim(trainData)## Skim summary statistics
## n obs: 803
## n variables: 18
##
## ── Variable type:factor ──────────────────────────────────────────────────────────────────────────────────────────────────────────
## variable missing complete n n_unique top_counts ordered
## Purchase 0 803 803 2 CH: 490, MM: 313, NA: 0 FALSE
## Store7 0 803 803 2 No: 529, Yes: 274, NA: 0 FALSE
## StoreID 1 802 803 5 7: 273, 2: 161, 3: 153, 1: 114 FALSE
##
## ── Variable type:numeric ─────────────────────────────────────────────────────────────────────────────────────────────────────────
## variable missing complete n mean sd p0 p25 p50 p75 p100 hist
## DiscCH 1 802 803 0.056 0.12 0 0 0 0 0.5 ▇▁▁▁▁▁▁▁
## DiscMM 4 799 803 0.12 0.21 0 0 0 0.2 0.8 ▇▁▁▁▁▁▁▁
## ListPriceDiff 0 803 803 0.22 0.11 0 0.14 0.24 0.3 0.44 ▂▂▂▁▇▆▁▁
## LoyalCH 5 798 803 0.56 0.31 1.1e-05 0.32 0.59 0.85 1 ▅▃▃▃▆▅▅▇
## PctDiscCH 1 802 803 0.029 0.065 0 0 0 0 0.25 ▇▁▁▁▁▁▁▁
## PctDiscMM 4 799 803 0.058 0.1 0 0 0 0.11 0.4 ▇▁▁▂▁▁▁▁
## PriceCH 1 802 803 1.87 0.1 1.69 1.79 1.86 1.99 2.09 ▂▅▁▇▁▁▅▁
## PriceDiff 1 802 803 0.16 0.27 -0.67 0 0.24 0.32 0.64 ▁▁▂▂▃▇▅▂
## PriceMM 1 802 803 2.09 0.13 1.69 2.09 2.13 2.18 2.29 ▁▁▁▃▁▇▃▂
## SalePriceCH 0 803 803 1.81 0.15 1.39 1.75 1.86 1.89 2.09 ▁▁▁▂▆▇▅▁
## SalePriceMM 4 799 803 1.97 0.25 1.19 1.69 2.09 2.18 2.29 ▁▁▃▃▁▂▇▆
## SpecialCH 2 801 803 0.15 0.36 0 0 0 0 1 ▇▁▁▁▁▁▁▂
## SpecialMM 3 800 803 0.17 0.37 0 0 0 0 1 ▇▁▁▁▁▁▁▂
## STORE 2 801 803 1.61 1.43 0 0 2 3 4 ▇▃▁▅▁▅▁▃
## WeekofPurchase 0 803 803 254.51 15.39 227 240 257 268 278 ▆▅▅▃▆▇▇▇Impute Missing Values
This data contains a fair amount of missing data points. There are a few way to impute missing values:
- If categorical data, fill in the category that appears most often (i.e. the mode).
- If numerical/continuous, fill in with the mean of the column.
- Predict the missing values using a predictive algorithm.
We will focus on the last point and use k Nearest Neighbors algorithm to fill in the blanks.
Before we continue, we should note the one missing StoreID row. We should expand it as a series of dummy one-hot columns:
dmy <- dummyVars(Purchase ~ ., data = trainData)
trainData_dmy <- data.frame(predict(dmy, newdata = trainData))## Warning in model.frame.default(Terms, newdata, na.action = na.action, xlev = object$lvls): variable
## 'Purchase' is not a factorskim(trainData_dmy)## Skim summary statistics
## n obs: 803
## n variables: 22
##
## ── Variable type:numeric ─────────────────────────────────────────────────────────────────────────────────────────────────────────
## variable missing complete n mean sd p0 p25 p50 p75 p100 hist
## DiscCH 1 802 803 0.056 0.12 0 0 0 0 0.5 ▇▁▁▁▁▁▁▁
## DiscMM 4 799 803 0.12 0.21 0 0 0 0.2 0.8 ▇▁▁▁▁▁▁▁
## ListPriceDiff 0 803 803 0.22 0.11 0 0.14 0.24 0.3 0.44 ▂▂▂▁▇▆▁▁
## LoyalCH 5 798 803 0.56 0.31 1.1e-05 0.32 0.59 0.85 1 ▅▃▃▃▆▅▅▇
## PctDiscCH 1 802 803 0.029 0.065 0 0 0 0 0.25 ▇▁▁▁▁▁▁▁
## PctDiscMM 4 799 803 0.058 0.1 0 0 0 0.11 0.4 ▇▁▁▂▁▁▁▁
## PriceCH 1 802 803 1.87 0.1 1.69 1.79 1.86 1.99 2.09 ▂▅▁▇▁▁▅▁
## PriceDiff 1 802 803 0.16 0.27 -0.67 0 0.24 0.32 0.64 ▁▁▂▂▃▇▅▂
## PriceMM 1 802 803 2.09 0.13 1.69 2.09 2.13 2.18 2.29 ▁▁▁▃▁▇▃▂
## SalePriceCH 0 803 803 1.81 0.15 1.39 1.75 1.86 1.89 2.09 ▁▁▁▂▆▇▅▁
## SalePriceMM 4 799 803 1.97 0.25 1.19 1.69 2.09 2.18 2.29 ▁▁▃▃▁▂▇▆
## SpecialCH 2 801 803 0.15 0.36 0 0 0 0 1 ▇▁▁▁▁▁▁▂
## SpecialMM 3 800 803 0.17 0.37 0 0 0 0 1 ▇▁▁▁▁▁▁▂
## STORE 2 801 803 1.61 1.43 0 0 2 3 4 ▇▃▁▅▁▅▁▃
## Store7.No 0 803 803 0.66 0.47 0 0 1 1 1 ▅▁▁▁▁▁▁▇
## Store7.Yes 0 803 803 0.34 0.47 0 0 0 1 1 ▇▁▁▁▁▁▁▅
## StoreID.1 1 802 803 0.14 0.35 0 0 0 0 1 ▇▁▁▁▁▁▁▁
## StoreID.2 1 802 803 0.2 0.4 0 0 0 0 1 ▇▁▁▁▁▁▁▂
## StoreID.3 1 802 803 0.19 0.39 0 0 0 0 1 ▇▁▁▁▁▁▁▂
## StoreID.4 1 802 803 0.13 0.33 0 0 0 0 1 ▇▁▁▁▁▁▁▁
## StoreID.7 1 802 803 0.34 0.47 0 0 0 1 1 ▇▁▁▁▁▁▁▅
## WeekofPurchase 0 803 803 254.51 15.39 227 240 257 268 278 ▆▅▅▃▆▇▇▇caret::preProcess()
This command creates a model that can be used to impute missing values. Let’s create a preProcess model that uses knn. Note that preProcess only works on numeric data, so by default our three factored columns (Purchased, StoreID, Store7) will be ignored.
# Create the knn imputation model on the training data
impute_missing_model <- preProcess(trainData_dmy, method='knnImpute')
impute_missing_model## Created from 774 samples and 22 variables
##
## Pre-processing:
## - centered (22)
## - ignored (0)
## - 5 nearest neighbor imputation (22)
## - scaled (22)The above output shows the various preprocessing steps done in the process of knn imputation.
That is, it has centered (subtract by mean) 22 variables, ignored 0, used k=5 (considered 5 nearest neighbors) to predict the missing values and finally scaled (divide by standard deviation) 22 variables.
Let’s now use this model to predict the missing values in trainData:
# Use the imputation model to predict the values of missing data points
library(RANN) # required for knnInpute
trainData_impute <- predict(impute_missing_model, newdata = trainData_dmy)
# check if any NA values exist
if (!anyNA(trainData_impute)){
message("All missing values have been filled in...good job!")
} else if (anyNA(trainData_impute)){
message("Missing data still exists...try again!")
}## All missing values have been filled in...good job!recipes::recipe(), prep(), bake()
In caret, you determine what imputing algorithm you’re going to use, then you run it. Within the tidymodels universe, you instead create a recipe(). Think of it exactly as the name implies, you are designing a recipe to cook something…but not cooking it just yet. There are things you can still tweak in your recipe() before actually popping it in the oven to bake(). Let’ go ahead and add in a pre-processing step to impute our missing data with knn within our recipe. The recipe must start with a formula. For this example, we are going to predict Purchase using all predictors:
# Add forumla to recipe
orange_recipe <- recipe(Purchase ~ ., data = trainData)
summary(orange_recipe)## # A tibble: 18 x 4
## variable type role source
## <chr> <chr> <chr> <chr>
## 1 WeekofPurchase numeric predictor original
## 2 StoreID nominal predictor original
## 3 PriceCH numeric predictor original
## 4 PriceMM numeric predictor original
## 5 DiscCH numeric predictor original
## 6 DiscMM numeric predictor original
## 7 SpecialCH numeric predictor original
## 8 SpecialMM numeric predictor original
## 9 LoyalCH numeric predictor original
## 10 SalePriceMM numeric predictor original
## 11 SalePriceCH numeric predictor original
## 12 PriceDiff numeric predictor original
## 13 Store7 nominal predictor original
## 14 PctDiscMM numeric predictor original
## 15 PctDiscCH numeric predictor original
## 16 ListPriceDiff numeric predictor original
## 17 STORE numeric predictor original
## 18 Purchase nominal outcome originalThe order in which you infer, center, scale, etc does matter (see this post).
Impute
Individual transformations for skewness and other issues
Discretize (if needed and if you have no other choice)
Create dummy variables
Create interactions
Normalization steps (center, scale, range, etc)
Multivariate transformation (e.g. PCA, spatial sign, etc)
# Add imputing steps to recipe
orange_recipe_steps <- orange_recipe %>%
# Add dummy variables for "class" variables
step_dummy(Store7, StoreID, one_hot = TRUE) %>%
# knn impute all variables
step_knnimpute(all_predictors()) %>%
# Center and Scale
step_center(all_predictors()) %>%
step_scale(all_predictors())
orange_recipe_steps## Data Recipe
##
## Inputs:
##
## role #variables
## outcome 1
## predictor 17
##
## Operations:
##
## Dummy variables from Store7, StoreID
## 5-nearest neighbor imputation for all_predictors
## Centering for all_predictors
## Scaling for all_predictorsNow that the recipe is finished, you can see from the output exactly what is going into the recipe. It’s important to note that at this point, nothing has been imputed or transformed.
Next, we need to see how this recipe will work on our data set. prep() will perform the various recipe steps on our training data and calculate the necessary statistics (eg. means and standar deviations):
prepped_recipe <- prep(orange_recipe_steps, training = trainData)## Warning: There are new levels in a factor: NAprepped_recipe## Data Recipe
##
## Inputs:
##
## role #variables
## outcome 1
## predictor 17
##
## Training data contained 803 data points and 29 incomplete rows.
##
## Operations:
##
## Dummy variables from Store7, StoreID [trained]
## 5-nearest neighbor imputation for PriceCH, PriceMM, DiscCH, DiscMM, SpecialCH, SpecialMM, ... [trained]
## Centering for WeekofPurchase, PriceCH, PriceMM, DiscCH, DiscMM, ... [trained]
## Scaling for WeekofPurchase, PriceCH, PriceMM, DiscCH, DiscMM, ... [trained]You can see here from the output that for each imputation/tranformation what columns are impacted. We can now
We can now apply our prepped recipe to the training data:
trainData_baked <- bake(prepped_recipe, new_data = trainData) # convert to the train data to the newly imputed data## Warning: There are new levels in a factor: NAtestData_baked <- bake(prepped_recipe, new_data = testData) # do the same for the test data
skim(trainData_baked)## Skim summary statistics
## n obs: 803
## n variables: 23
##
## ── Variable type:factor ──────────────────────────────────────────────────────────────────────────────────────────────────────────
## variable missing complete n n_unique top_counts ordered
## Purchase 0 803 803 2 CH: 490, MM: 313, NA: 0 FALSE
##
## ── Variable type:numeric ─────────────────────────────────────────────────────────────────────────────────────────────────────────
## variable missing complete n mean sd p0 p25 p50 p75 p100 hist
## DiscCH 0 803 803 2.5e-17 1 -0.46 -0.46 -0.46 -0.46 3.64 ▇▁▁▁▁▁▁▁
## DiscMM 0 803 803 -2.6e-17 1 -0.57 -0.57 -0.57 0.38 3.24 ▇▁▁▁▁▁▁▁
## ListPriceDiff 0 803 803 -1.3e-16 1 -2.05 -0.74 0.19 0.75 2.05 ▂▂▁▁▇▆▁▁
## LoyalCH 0 803 803 -1.1e-16 1 -1.79 -0.76 0.1 0.92 1.42 ▅▃▃▃▆▅▅▇
## PctDiscCH 0 803 803 2.5e-17 1 -0.46 -0.46 -0.46 -0.46 3.46 ▇▁▁▁▁▁▁▁
## PctDiscMM 0 803 803 -7.6e-18 1 -0.58 -0.58 -0.58 0.55 3.44 ▇▁▁▂▁▁▁▁
## PriceCH 0 803 803 -2.7e-16 1 -1.75 -0.77 -0.082 1.19 2.17 ▂▃▂▇▁▁▆▁
## PriceDiff 0 803 803 -3.3e-17 1 -3.04 -0.57 0.31 0.61 1.78 ▁▁▂▂▃▇▅▂
## PriceMM 0 803 803 -4.8e-16 1 -2.99 0.013 0.31 0.69 1.51 ▁▁▁▃▁▇▃▂
## SalePriceCH 0 803 803 -3e-16 1 -2.89 -0.43 0.32 0.53 1.9 ▁▁▁▂▆▇▅▁
## SalePriceMM 0 803 803 -4.1e-16 1 -3.1 -1.11 0.48 0.84 1.28 ▁▁▃▃▁▂▇▆
## SpecialCH 0 803 803 -5.1e-17 1 -0.42 -0.42 -0.42 -0.42 2.36 ▇▁▁▁▁▁▁▂
## SpecialMM 0 803 803 2.6e-18 1 -0.45 -0.45 -0.45 -0.45 2.22 ▇▁▁▁▁▁▁▂
## STORE 0 803 803 1.6e-17 1 -1.13 -1.13 0.27 0.96 1.66 ▇▃▁▅▁▅▁▃
## Store7_No 0 803 803 8.2e-17 1 -1.39 -1.39 0.72 0.72 0.72 ▅▁▁▁▁▁▁▇
## Store7_Yes 0 803 803 -9.3e-18 1 -0.72 -0.72 -0.72 1.39 1.39 ▇▁▁▁▁▁▁▅
## StoreID_X1 0 803 803 -1.4e-17 1 -0.41 -0.41 -0.41 -0.41 2.46 ▇▁▁▁▁▁▁▁
## StoreID_X2 0 803 803 -2.2e-17 1 -0.5 -0.5 -0.5 -0.5 2 ▇▁▁▁▁▁▁▂
## StoreID_X3 0 803 803 1.2e-17 1 -0.48 -0.48 -0.48 -0.48 2.06 ▇▁▁▁▁▁▁▂
## StoreID_X4 0 803 803 -1.8e-17 1 -0.38 -0.38 -0.38 -0.38 2.63 ▇▁▁▁▁▁▁▁
## StoreID_X7 0 803 803 -9.3e-18 1 -0.72 -0.72 -0.72 1.39 1.39 ▇▁▁▁▁▁▁▅
## WeekofPurchase 0 803 803 -5.8e-16 1 -1.79 -0.94 0.16 0.88 1.53 ▆▅▅▃▆▇▇▇The data is now in a form where all missing values have been imputed, all factor/nominal columns have been one-hot encoded, and is now ready for analysis!
Feature Analysis
Before you even make prediction, sometimes (if you data doesn’t have 1000000… columns), you can just look to see how the features differ between the categories you are trying to predict.
caret::featurePlot()
Let’ make some various plots to see how the preditor data is distibuted between CH and MM:
featurePlot(x = trainData_baked[, 2:23],
y = trainData_baked$Purchase,
plot = "box",
strip=strip.custom(par.strip.text=list(cex=.7)),
scales = list(x = list(relation="free"),
y = list(relation="free")))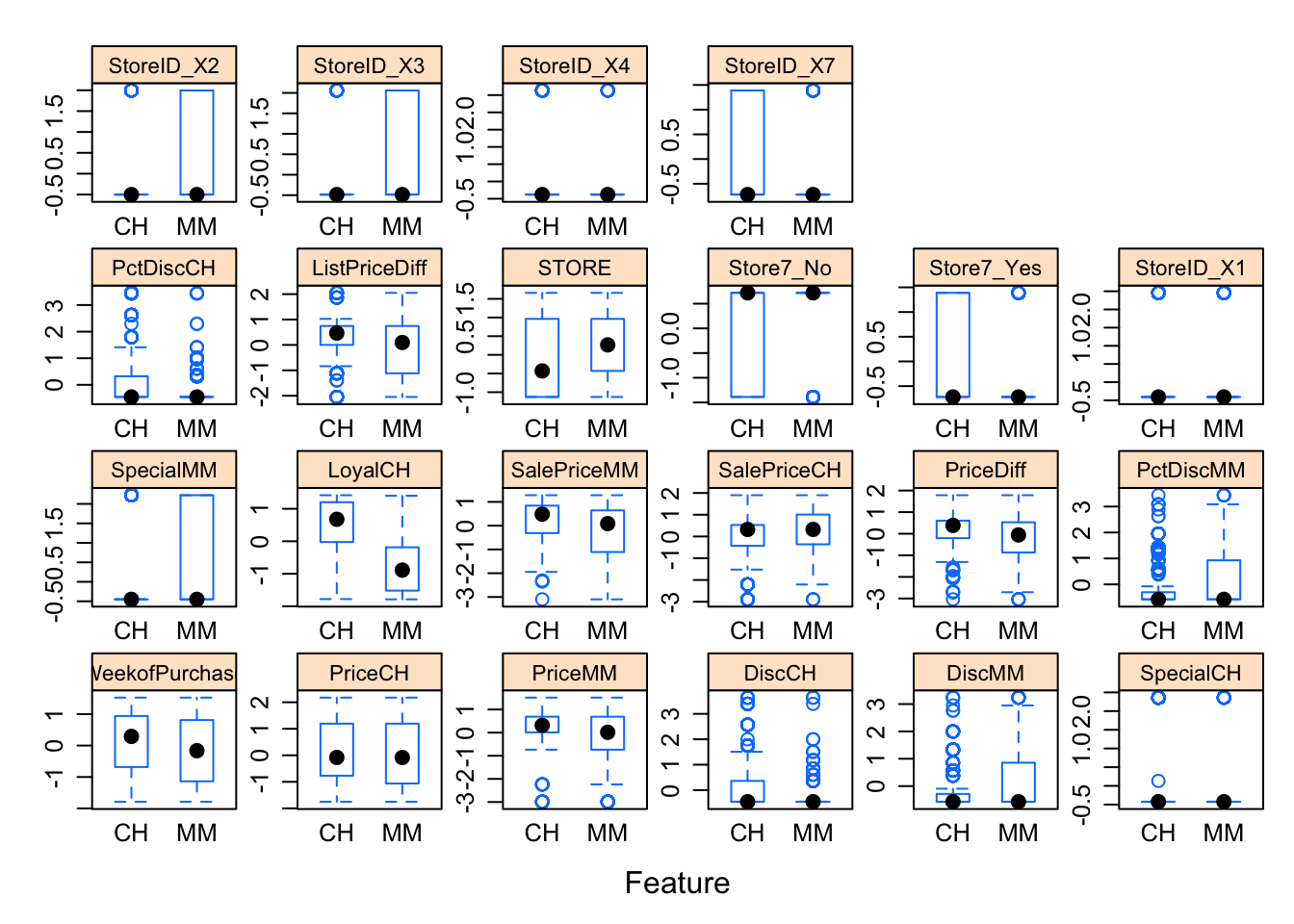
featurePlot(x = trainData_baked[, 2:23],
y = trainData_baked$Purchase,
plot = "density",
strip=strip.custom(par.strip.text=list(cex=.7)),
scales = list(x = list(relation="free"),
y = list(relation="free")))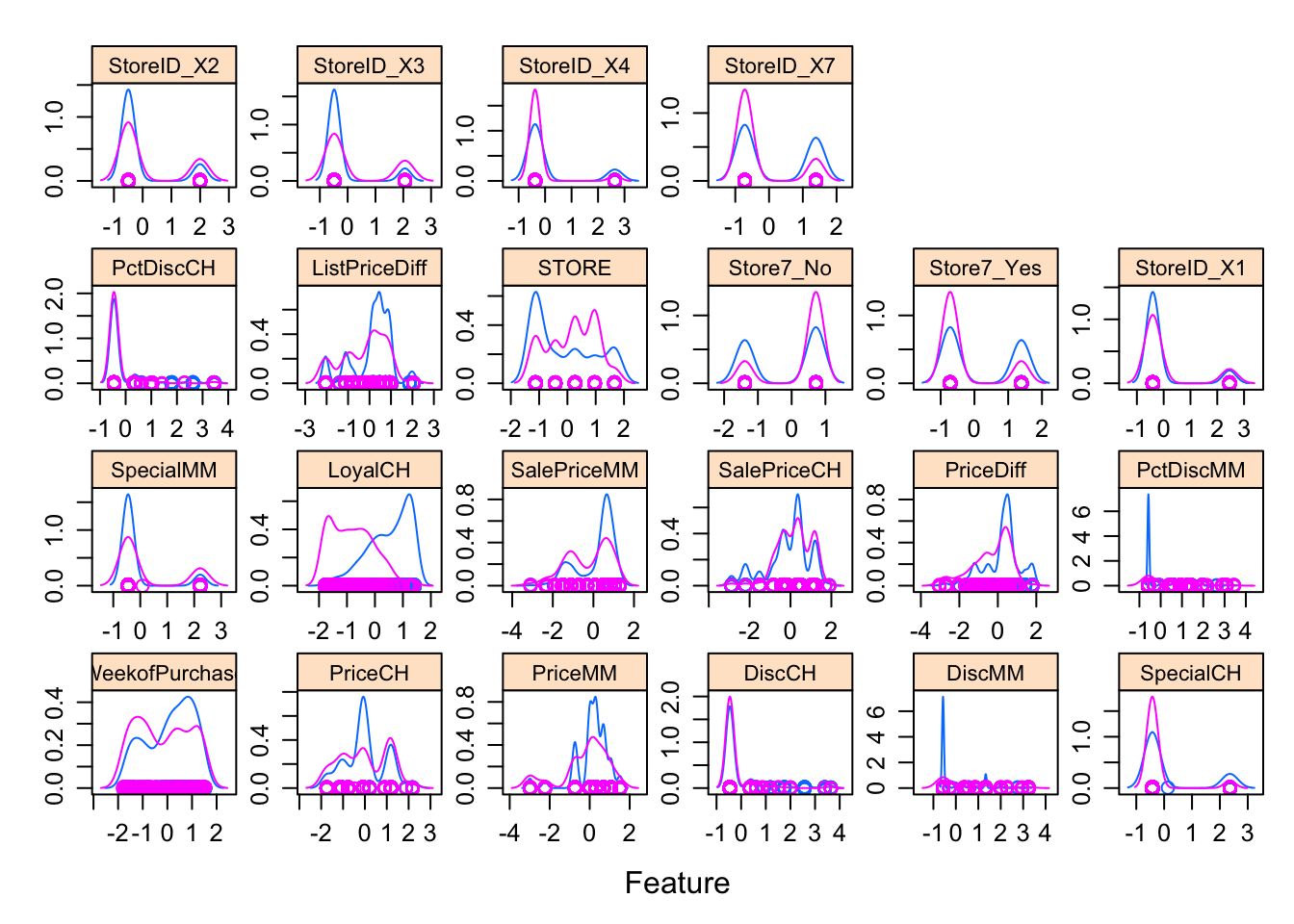
Tidymodels feature plots (using Tidyverse)
I don’t believe there are any quick functions built into the tidymodels packages to make quick feature plots, but this is pricicely what makes it good…it’s not too specific and plays well with other packages within the tidyverse. Here I’ll use ggplot, purrr, and cowplot to make similar boxplots and density plots.
box_fun_plot = function(data, x, y) {
ggplot(data = data, aes(x = .data[[x]],
y = .data[[y]],
fill = .data[[x]])) +
geom_boxplot() +
labs(title = y,
x = x,
y = y) +
theme(
legend.position = "none"
)
}
# Create vector of predictors
expl <- names(trainData_baked)[-1]
# Loop vector with map
expl_plots_box <- map(expl, ~box_fun_plot(data = trainData_baked, x = "Purchase", y = .x) )
plot_grid(plotlist = expl_plots_box)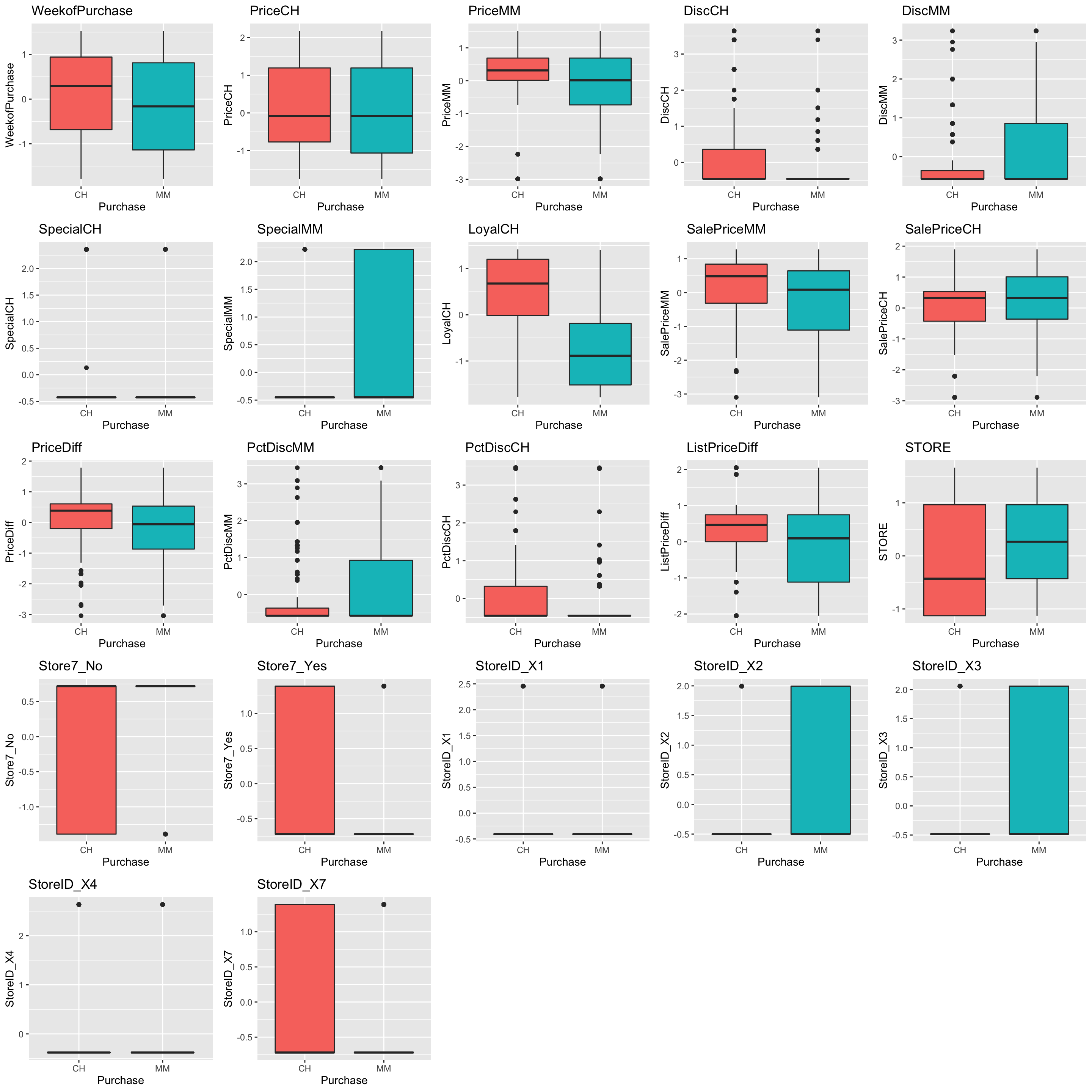
density_fun_plot = function(data, x, y) {
ggplot(data = data, aes(x = .data[[y]],
fill = .data[[x]])) +
geom_density(alpha = 0.7) +
labs(title = y,
x = y) +
theme(
legend.position = "none"
)
}
# Loop vector with map
expl_plots_density <- map(expl, ~density_fun_plot(data = trainData_baked, x = "Purchase", y = .x) )
plot_grid(plotlist = expl_plots_density)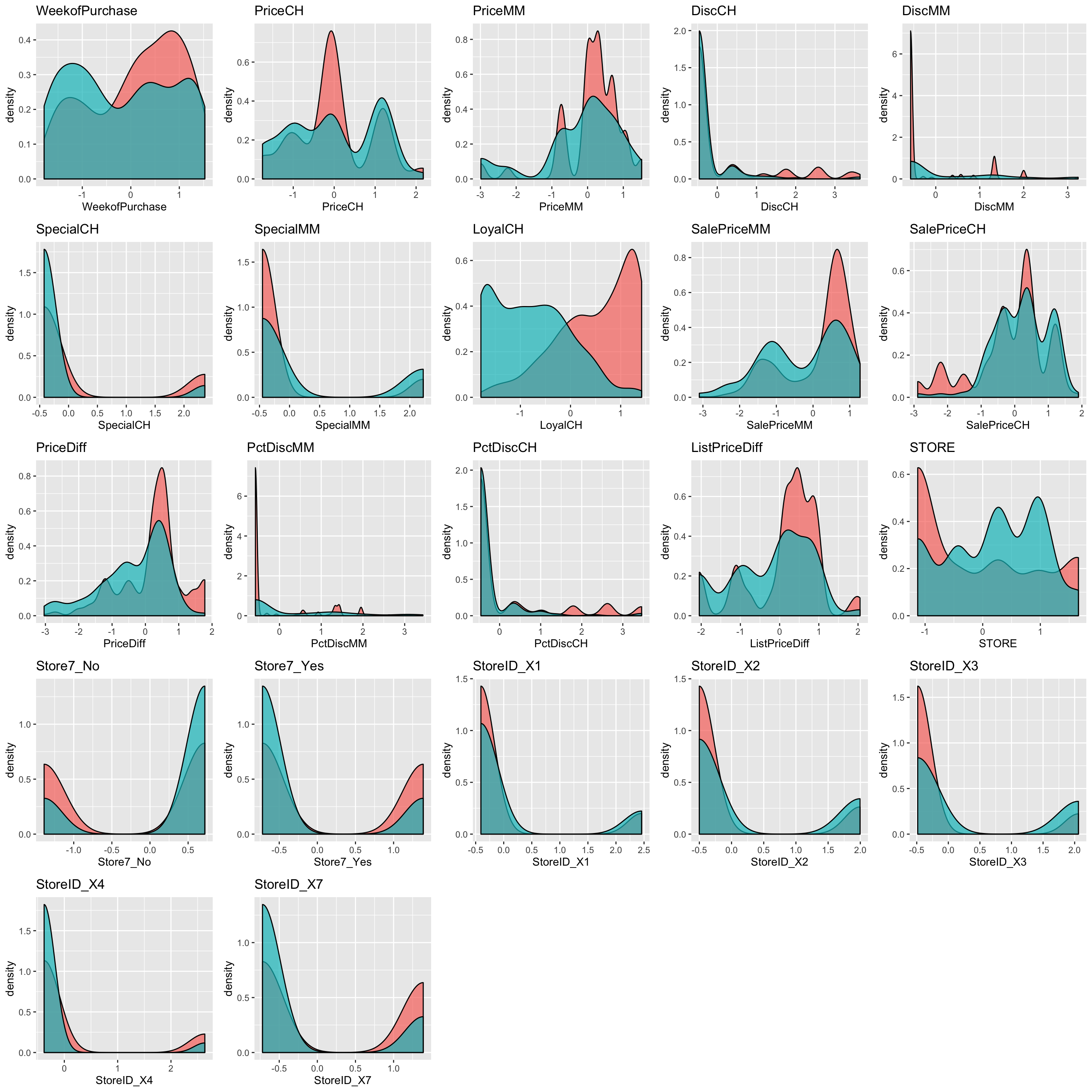
Training Models
There are tons of machine learning algorithms out there, but to keep things simple, we are going to fit a randomForest model to the data. Let’s first discuss how to do this in caret
caret::trainControl(), train()
trainControl() allows us to specify how we want to train the model. Do we want to do cross validation? Reapeated cross validation? Bootstrapping? How many repetitions? All of these things get specified in trainControl(). With randomForest (from the ranger package), there is one parameter that needs tuning: mtry (number of variables randomly sampled as candidates at each split).
# Let's do 5 fold cross validation. This randomly splits the data into 5 parts, trains the model on 4 parts
# and validates on the remaining 1 part. It is recommended to use repeatedcv so you can repeat this process
# but for sake of computational time, will stick with cv.
train_control <- trainControl(method = "cv", number = 5)
# Run random forest using the ranger package
set.seed(1234)
rf_fit <- train(Purchase ~ ., # Predict purchase using all predictors
data = trainData_baked,
method = "ranger",
trControl = train_control)
rf_fit## Random Forest
##
## 803 samples
## 22 predictor
## 2 classes: 'CH', 'MM'
##
## No pre-processing
## Resampling: Cross-Validated (5 fold)
## Summary of sample sizes: 642, 643, 643, 642, 642
## Resampling results across tuning parameters:
##
## mtry splitrule Accuracy Kappa
## 2 gini 0.7894643 0.5449255
## 2 extratrees 0.7683075 0.4961147
## 12 gini 0.8106211 0.6022994
## 12 extratrees 0.7981366 0.5726823
## 22 gini 0.8106289 0.6025827
## 22 extratrees 0.8006444 0.5784234
##
## Tuning parameter 'min.node.size' was held constant at a value of 1
## Accuracy was used to select the optimal model using the largest value.
## The final values used for the model were mtry = 22, splitrule = gini and min.node.size = 1.By default, the tuning parameter mtry goes through 3 iterations (2, 12, and 22…based on size of dataset). You can define your own tuning grid as well. Let’s make one and expand the parameters using mtry, splitrule, and min.node.size which determines the minimum size of each terminal node in tree. A value of one make lead to overfitting/really large trees.
You can also give the train() command a preProcess argument where you can define various tools to pre-process the training data. Since we already did that previously, we don’t need to hear, but it’s an option you should be aware of.
rf_grid <- expand.grid(mtry = c(2, 5, 10, 20),
splitrule = c("gini", "extratrees"),
min.node.size = c(1, 3, 5))
# Train new model using grid
set.seed(1234)
rf_fit_grid <- train(Purchase ~ .,
data = trainData_baked,
method = "ranger",
trControl = train_control,
tuneGrid = rf_grid)
rf_fit_grid## Random Forest
##
## 803 samples
## 22 predictor
## 2 classes: 'CH', 'MM'
##
## No pre-processing
## Resampling: Cross-Validated (5 fold)
## Summary of sample sizes: 642, 643, 643, 642, 642
## Resampling results across tuning parameters:
##
## mtry splitrule min.node.size Accuracy Kappa
## 2 gini 1 0.7844876 0.5351284
## 2 gini 3 0.7894643 0.5472036
## 2 gini 5 0.7907143 0.5507238
## 2 extratrees 1 0.7707842 0.5018237
## 2 extratrees 3 0.7670730 0.4939358
## 2 extratrees 5 0.7658230 0.4907856
## 5 gini 1 0.8180745 0.6143151
## 5 gini 3 0.8218323 0.6216923
## 5 gini 5 0.8156134 0.6089515
## 5 extratrees 1 0.7969177 0.5661397
## 5 extratrees 3 0.8056134 0.5834305
## 5 extratrees 5 0.8043789 0.5810045
## 10 gini 1 0.8131134 0.6067557
## 10 gini 3 0.8180978 0.6185068
## 10 gini 5 0.8118866 0.6056586
## 10 extratrees 1 0.7969099 0.5689128
## 10 extratrees 3 0.8031366 0.5828258
## 10 extratrees 5 0.8056289 0.5880113
## 20 gini 1 0.8093944 0.6002265
## 20 gini 3 0.8143556 0.6100268
## 20 gini 5 0.8156134 0.6134386
## 20 extratrees 1 0.8018789 0.5819375
## 20 extratrees 3 0.8031599 0.5855577
## 20 extratrees 5 0.8081599 0.5961990
##
## Accuracy was used to select the optimal model using the largest value.
## The final values used for the model were mtry = 5, splitrule = gini and min.node.size = 3.You can see that the best model was an mtry of 10, splitrule of extratrees and a minimun node size of 5.
parsnip
In tidymodels, training models is done using the parsnip package. Let’s start small and simply establish that we want to train a random forest model. We won’t specify any parameters or packages that run randomforest. Just simply “I want random forest”:
# Set model to random forest
rf_mod <- rand_forest()
rf_mod## Random Forest Model Specification (unknown)Similar to the recipe() command above, we can now start adding various parameters to our model. To see what parameters exist, you can run the arg() command:
args(rand_forest)## function (mode = "unknown", mtry = NULL, trees = NULL, min_n = NULL)
## NULLJust like above, you may want to tune the various parameters. You can use varying() as a place holder for parameters you want to tune later. We also want to tell the model we are trying to predict MM vs CH, which is a classification problem. We are also going to use ranger (just like above) and set the seed internally.
rf_mod <-
rand_forest(mtry = varying(), mode = "classification") %>%
set_engine("ranger", seed = 1234)
rf_mod## Random Forest Model Specification (classification)
##
## Main Arguments:
## mtry = varying()
##
## Engine-Specific Arguments:
## seed = 1234
##
## Computational engine: rangerLet’s try running the model with an mtry of 5.
rf_mod %>%
set_args(mtry = 5) %>%
fit(Purchase ~ ., data = trainData_baked)## parsnip model object
##
## Ranger result
##
## Call:
## ranger::ranger(formula = formula, data = data, mtry = ~5, seed = ~1234, num.threads = 1, verbose = FALSE, probability = TRUE)
##
## Type: Probability estimation
## Number of trees: 500
## Sample size: 803
## Number of independent variables: 22
## Mtry: 5
## Target node size: 10
## Variable importance mode: none
## Splitrule: gini
## OOB prediction error (Brier s.): 0.1318658Now, what if we wanted to do cross-validation? We need to go back to rsample package for this. This may seem like a little more work than what was presented in the caret part, but in a way it gives you a little more control over your data and ensures you know exactly what your doing each step of the way.
set.seed(1234)
# Create a 5 fold cross validation dat set
cv_splits <- vfold_cv(
data = trainData_baked,
v = 5,
strata = "Purchase"
)
cv_splits## # 5-fold cross-validation using stratification
## # A tibble: 5 x 2
## splits id
## <named list> <chr>
## 1 <split [642/161]> Fold1
## 2 <split [642/161]> Fold2
## 3 <split [642/161]> Fold3
## 4 <split [643/160]> Fold4
## 5 <split [643/160]> Fold5The splits row contains how the data will be split within each fold (4/5 of the data will be in one group, 1/5 in the other). Let’s look a the first fold just to see how the data will be split:
cv_splits$splits[[1]]## <642/161/803># This will extract the 4/5ths analysis data part
cv_splits$splits[[1]] %>% analysis() %>% dim()## [1] 642 23# This will extract the 1/5th assessment data part
cv_splits$splits[[1]] %>% assessment() %>% dim()## [1] 161 23Now I need to create a function that contains my model that can be iterated over each split of the data. I also want a function that will make predictions using said model.
fit_mod_func <- function(split, spec){
fit(object = spec,
formula = Purchase ~ .,
data = analysis(split))
}
predict_func <- function(split, model){
# Extract the assessment data
assess <- assessment(split)
# Make prediction
pred <- predict(model, new_data = assess)
as_tibble(cbind(assess, pred[[1]]))
}Then, using the purrr::map() function, iterate the function over each fold of the data. This will create a random forest model for each fold of the data. Store the results in a new column in cv_splits.
spec_rf <- rand_forest() %>%
set_engine("ranger")
cv_splits <- cv_splits %>%
mutate(models_rf = map(.x = splits, .f = fit_mod_func, spec = spec_rf))
cv_splits## # 5-fold cross-validation using stratification
## # A tibble: 5 x 3
## splits id models_rf
## * <named list> <chr> <named list>
## 1 <split [642/161]> Fold1 <fit[+]>
## 2 <split [642/161]> Fold2 <fit[+]>
## 3 <split [642/161]> Fold3 <fit[+]>
## 4 <split [643/160]> Fold4 <fit[+]>
## 5 <split [643/160]> Fold5 <fit[+]>We can then inspect each model if you wanted:
cv_splits$models_rf[[1]]## parsnip model object
##
## Ranger result
##
## Call:
## ranger::ranger(formula = formula, data = data, num.threads = 1, verbose = FALSE, seed = sample.int(10^5, 1))
##
## Type: Classification
## Number of trees: 500
## Sample size: 642
## Number of independent variables: 22
## Mtry: 4
## Target node size: 1
## Variable importance mode: none
## Splitrule: gini
## OOB prediction error: 16.36 %Next, add a column that contains the predictions:
cv_splits <- cv_splits %>%
mutate(pred_rf = map2(.x = splits, .y = models_rf, .f = predict_func))
cv_splits## # 5-fold cross-validation using stratification
## # A tibble: 5 x 4
## splits id models_rf pred_rf
## * <named list> <chr> <named list> <named list>
## 1 <split [642/161]> Fold1 <fit[+]> <tibble [161 × 24]>
## 2 <split [642/161]> Fold2 <fit[+]> <tibble [161 × 24]>
## 3 <split [642/161]> Fold3 <fit[+]> <tibble [161 × 24]>
## 4 <split [643/160]> Fold4 <fit[+]> <tibble [160 × 24]>
## 5 <split [643/160]> Fold5 <fit[+]> <tibble [160 × 24]>To calculate performance metrics, we’ll create another function:
# Will calculate accuracy of classification
perf_metrics <- metric_set(accuracy)
# Create a function that will take the prediction and compare to truth
rf_metrics <- function(pred_df){
perf_metrics(
pred_df,
truth = Purchase,
estimate = res # res is the column name for the predictions
)
}
cv_splits <- cv_splits %>%
mutate(perf_rf = map(pred_rf, rf_metrics))Let’s take a look at the first fold’s accuracy:
cv_splits$perf_rf[[1]]## # A tibble: 1 x 3
## .metric .estimator .estimate
## <chr> <chr> <dbl>
## 1 accuracy binary 0.708We can also average the accuracy column to get the mean accuracy for all folds in the cross-valication:
cv_splits %>%
unnest(perf_rf) %>%
group_by(.metric) %>%
summarise(
.avg = mean(.estimate),
.sd = sd(.estimate)
)## # A tibble: 1 x 3
## .metric .avg .sd
## <chr> <dbl> <dbl>
## 1 accuracy 0.801 0.0593And there it is, we predicted if CM or MM with roughly 80% accuracy using random forest, but implementing it in two different environments: caret and tidymodels.
